DISEÑO DE CURVAS HORIZONTALES CIRCULARES
ELEMENTOS DE LA CURVA HORIZONTAL
CURVA SIMPLE

![ Tangente [T]: Distancia desde el punto de intersección de las tangentes (PI) -los
alineamientos rectos también se conoce...](https://image.slidesharecdn.com/elementosdelacurvacircularessimplesparaunavia-150126051508-conversion-gate02/95/elementos-de-la-curva-circulares-simples-para-una-via-2-638.jpg?cb=1422249371)
![ Ordenada Media [M] (o flecha [F]): Distancia desde el punto medio de la curva hasta
el punto medio de la cuerda larga.
𝑀...](https://image.slidesharecdn.com/elementosdelacurvacircularessimplesparaunavia-150126051508-conversion-gate02/95/elementos-de-la-curva-circulares-simples-para-una-via-3-638.jpg?cb=1422249371)


CURVA COMPUESTA




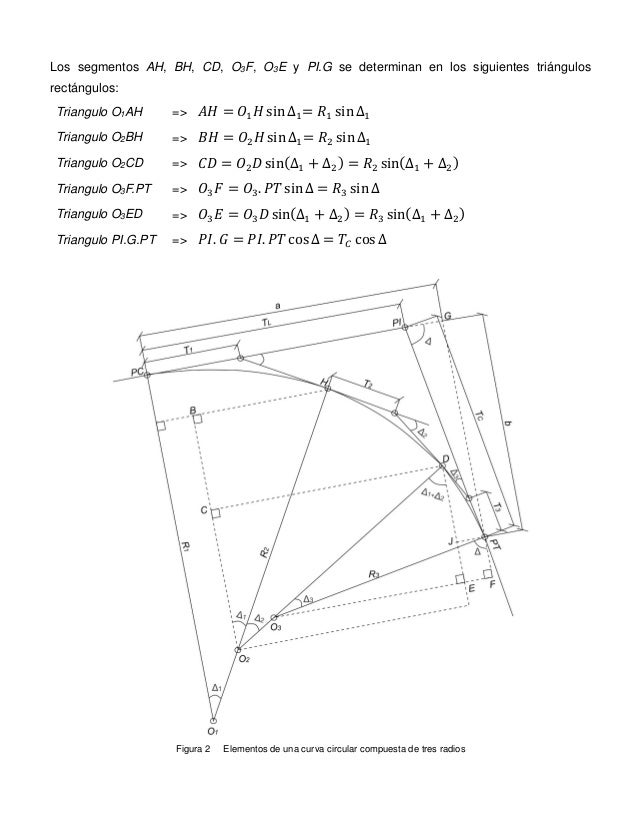
![Por lo tanto, en [1]:
𝑇𝑇𝐿𝐿 = 𝑅𝑅1 sin ∆1 − 𝑅𝑅2 sin ∆1 + 𝑅𝑅2 sin(∆1 + ∆2) + 𝑅𝑅3 sin ∆ − 𝑅𝑅3 sin(∆1 + ∆2) − 𝑇𝑇𝐶𝐶 cos ∆
𝑇𝑇𝐿𝐿 =...](https://image.slidesharecdn.com/curvascompuestas-robingomez9799075-160806002815/95/curvas-compuestas-robin-gomez-9799075-8-638.jpg?cb=1470443390)
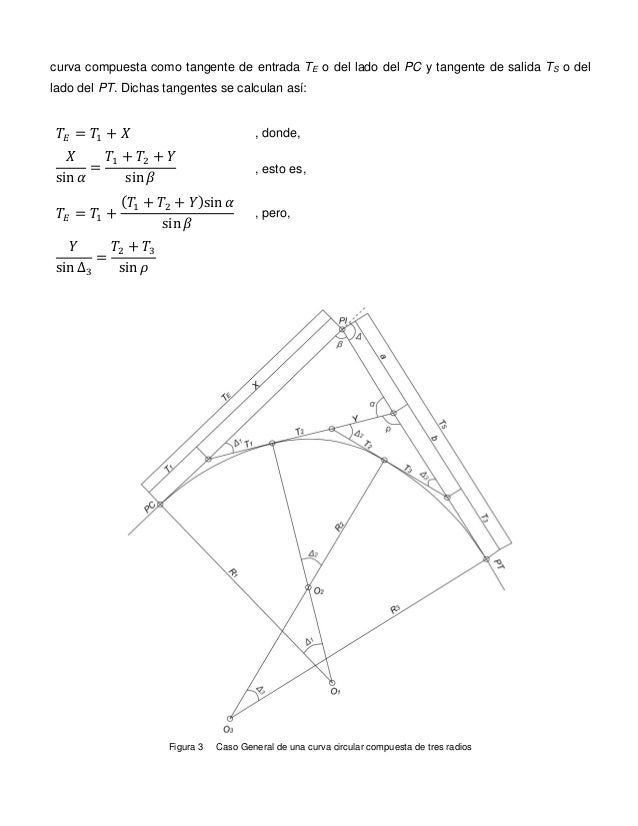
![La tangente larga TL se obtiene reemplazando la ecuación (1-01) en [2]:
𝑇𝑇𝐿𝐿 = (𝑅𝑅1 − 𝑅𝑅2) sin ∆1 + (𝑅𝑅2 − 𝑅𝑅3) sin(∆1 + ∆...](https://image.slidesharecdn.com/curvascompuestas-robingomez9799075-160806002815/95/curvas-compuestas-robin-gomez-9799075-9-638.jpg?cb=1470443390)

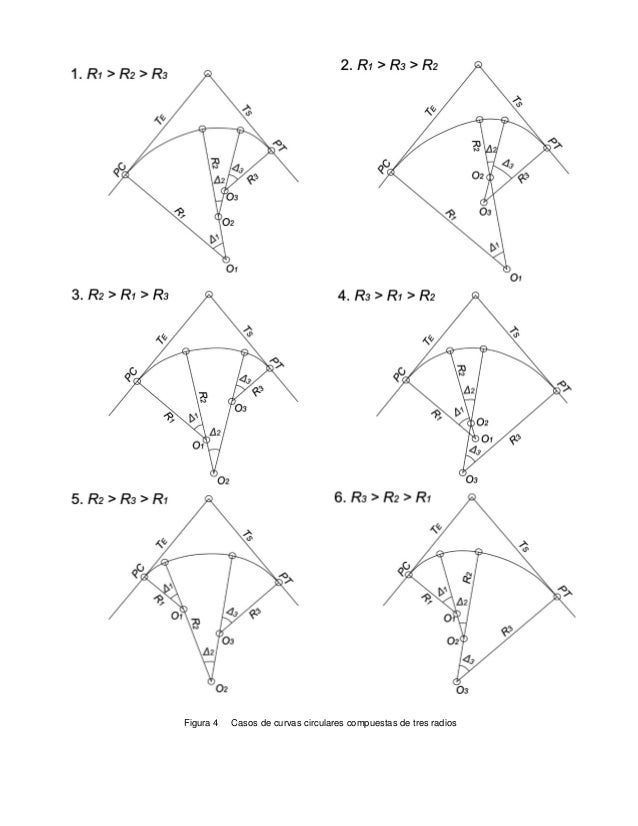
CURVA POLI CÉNTRICA

ESTACADO, REPLANTEO DE LA CURVA HORIZONTAL

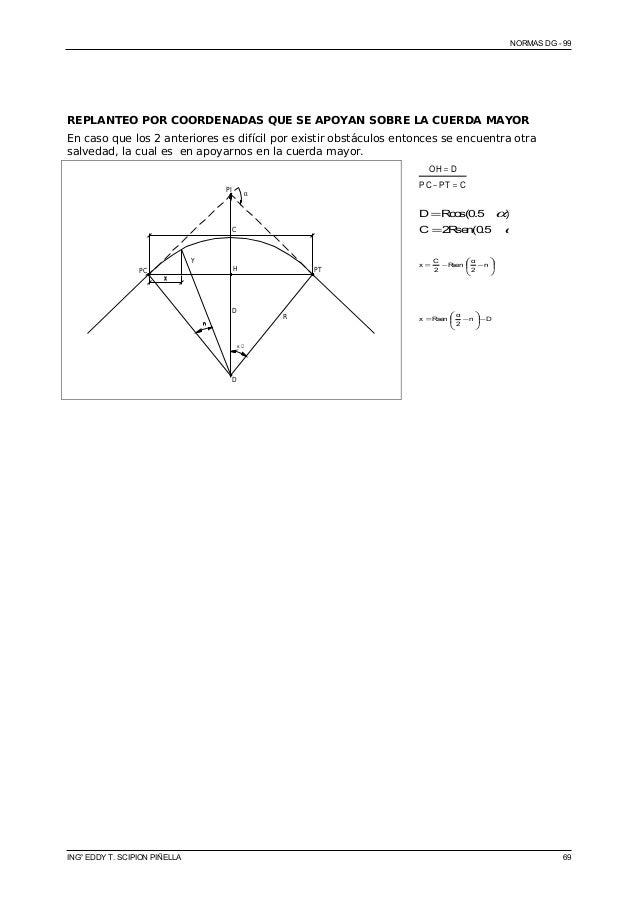
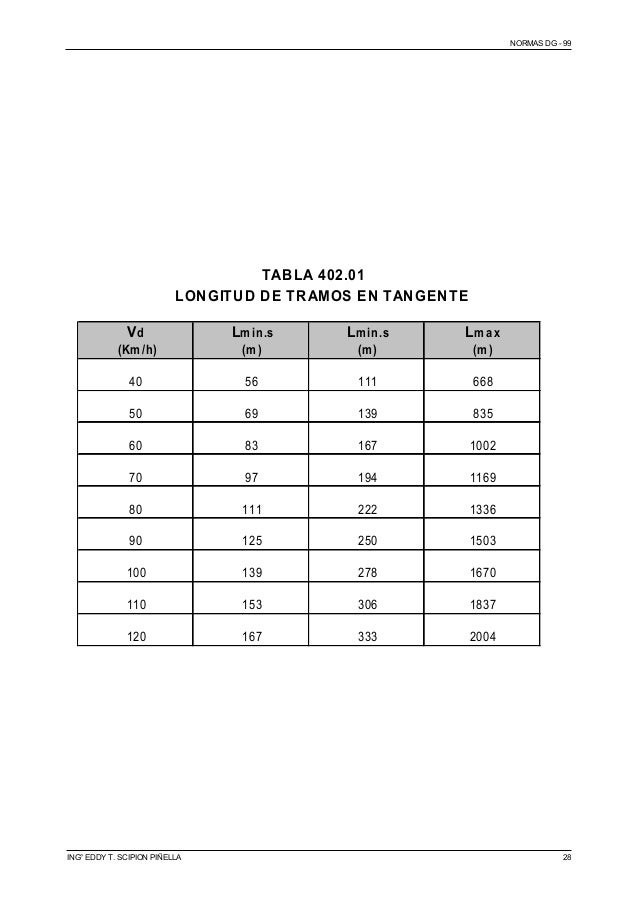
LONGITUD DE TRAMOS EN TANGENTE ENTRE CURVAS
TORTUOSIDAD DE LA VÍA.



- PC: es el punto de comienzo o inicio de la curva.
- PT: es el punto donde terminara la curva circular.
- PI: Punto donde se cortan los alineamientos rectos que van a ser empalmados por la curva. Intersección de tangentes.
- PM: Es el punto medio de la curva.
- E: Secante externa o simplemente Externa equivalente a la distancia desde el PI al PM.
- T: Tangente de la curva. Es el segmento de recta entre PC-PI y PT-PI el cual es simétrico.
- R: Radio de la curva. Este es perpendicular a PC y PT. Este se elige acorde al caso, tipo de camino, vehiculo, velocidad y otros más que estudiaremos posteriormente en el transcurso de nuestra carrera.
- D o LC: es el desarrollo de la curva o longitud sobre la curva el cual esta comprendido desde el PC al PT.
- CM: es la cuerda máxima dentro de la curva que va desde el PC al PT medida en línea recta.
- M: es la mediana de la curva la cual corresponde a la ordenada de al curva que une el al PM con el centro de la cuerda máxima.
- Δ: Es el ángulo central de la curva que es igual al ángulo de deflexión entre los dos alineamientos rectos y se puede calcular por la diferencia del azimut de llegada y el de salida.
- G°c: Este se define como un ángulo central que subtiende un arco de 20 m. Este y el Radio están siempre en razón inversa. El grado de curvatura Gc, está definido como el ángulo central que subtiende un arco de longitud establecida (LE), que para el caso de Nicaragua, se utiliza y/o está establecido de 20m.
De todos estos elementos se establecen las siguientes relaciones:
- Relación entre la tangente y el radio.
- Relación entre la curva máxima y el radio.
- Relación entre la mediana y el radio.
- Relación entre la externa y el radio.
- Relación entre el desarrollo y el radio.
- Grado de curvatura.

![ Tangente [T]: Distancia desde el punto de intersección de las tangentes (PI) -los
alineamientos rectos también se conoce...](https://image.slidesharecdn.com/elementosdelacurvacircularessimplesparaunavia-150126051508-conversion-gate02/95/elementos-de-la-curva-circulares-simples-para-una-via-2-638.jpg?cb=1422249371)
![ Ordenada Media [M] (o flecha [F]): Distancia desde el punto medio de la curva hasta
el punto medio de la cuerda larga.
𝑀...](https://image.slidesharecdn.com/elementosdelacurvacircularessimplesparaunavia-150126051508-conversion-gate02/95/elementos-de-la-curva-circulares-simples-para-una-via-3-638.jpg?cb=1422249371)







![Por lo tanto, en [1]:
𝑇𝑇𝐿𝐿 = 𝑅𝑅1 sin ∆1 − 𝑅𝑅2 sin ∆1 + 𝑅𝑅2 sin(∆1 + ∆2) + 𝑅𝑅3 sin ∆ − 𝑅𝑅3 sin(∆1 + ∆2) − 𝑇𝑇𝐶𝐶 cos ∆
𝑇𝑇𝐿𝐿 =...](https://image.slidesharecdn.com/curvascompuestas-robingomez9799075-160806002815/95/curvas-compuestas-robin-gomez-9799075-8-638.jpg?cb=1470443390)
![La tangente larga TL se obtiene reemplazando la ecuación (1-01) en [2]:
𝑇𝑇𝐿𝐿 = (𝑅𝑅1 − 𝑅𝑅2) sin ∆1 + (𝑅𝑅2 − 𝑅𝑅3) sin(∆1 + ∆...](https://image.slidesharecdn.com/curvascompuestas-robingomez9799075-160806002815/95/curvas-compuestas-robin-gomez-9799075-9-638.jpg?cb=1470443390)



CURVA POLI CÉNTRICA

ESTACADO, REPLANTEO DE LA CURVA HORIZONTAL


LONGITUD DE TRAMOS EN TANGENTE ENTRE CURVAS

TORTUOSIDAD DE LA VÍA.
Es una característica que representa lo tortuoso de una curva, es decir, el grado de vueltas o rodeos que tiene.
Existen varios intentos de medir este índice, aplicables a distintos escenarios.
TORTUOSIDAD DE LAS ROCAS
Uno de los factores geométricos que nos permiten caracterizar a las rocas porosas es la tortuosidad. Si se considera una muestra de roca con un camino poroso interconectado (como una arenisca) se puede definir la tortuosidad de la roca como:

Donde:
- es la longitud de la muestra de roca.
- es la longitud del camino electrolítico equivalente.
TORTUOSIDAD EN LECHOS RELLENOS
Es el cociente entre la longitud de las canales en el medio poroso (L') y la longitud del lecho (L):

Para evitar errores en el cálculo de la porosidad (e), normalmente se considera este cociente como 1, aunque en la realidad L' es mayor que L.




No hay comentarios.:
Publicar un comentario