TRAMO EN CURVA

DETERMINACIÓN DEL RADIO MÍNIMO: PROBLEMA DE DESLIZAMIENTO, PROBLEMA DE VUELCO.
INTRODUCCIÓN AL PERALTE.
Consiste en elevar en las curvas, el borde exterior de las vías una
cantidad, para que permita que una componente del vehículo se oponga a la
fuerza centrífuga (Fc) evitando de esta manera que el vehículo desvíe
radialmente su trayectoria hacia fuera.
GENERALIDADES:
Si se considera de una manera simplificada, las fuerzas que actúan sobre
un vehículo que se desplaza en una trayectoria curva horizontal, se observa que
la única fuerza que se opone al desplazamiento lateral del vehículo es la
fuerza de rozamiento que se desarrolla entre el neumático y el pavimento. La
fuerza de rozamiento no es suficiente para impedir el desplazamiento
transversal. Por ello para evitar que los vehículos de salgan de su trayectoria
es necesario que los componentes normales a la calzada sean siempre del mismo
sentido y se suman contribuyendo a la estabilidad del vehículo, en tanto que
las componentes paralelas a la calzada son de sentido opuesto y su relación
puede hacer variar los efectos que se sienten en el vehículo.
- PERALTE A PARTIR DEL DESLIZAMIENTO:
Una curva que no presenta peralte provoca el deslizamiento hacia fuera
de la vía y resulta inadecuado porque limita la velocidad en las curvas.
Por otra parte, ha quedado comprobado que cuando mayor sea el peralte
asignado a una curva que cruza a la izquierda, mayor es la dificultad de
maniobrar en la zona de transición.
- FORMAS DE REALIZAR EL PERALTE:
Existen cuatro métodos diferentes para la asignación del peralte a las
distintas curvas que se encuentran en un proyecto.
- El peralte se hace directamente proporcional al radio de la curva,
correspondiendo el valor del radio mínimo, el valor máximo del peralte. La
variación del coeficiente de rozamiento mantiene también una variación similar,
tanto para la velocidad del proyecto, como para la velocidad de circulación.
- El peralte es tal que un vehículo, viajando a la velocidad del proyecto,
tiene toda la fuerza centrífuga balanceado por el peralte, hasta requerirse el
máximo valor de éste, utilizándose el valor máximo del peralte solamente en las
curvas más cerradas.
- Se aplica el mismo procedimiento anterior, solo que para correlacionar
la velocidad en el peralte se utiliza la velocidad de circulación en vez de la
de proyecto. Este método trata de evitar las diferencias del método
anterior, variando el peralte en una velocidad menor que la del proyecto.
- Se mantiene una relación curvilínea (parabólica) entre los valores del peralte y los radios de la curva, con
valores comprendidos entre la que se obtiene según los métodos 1 y 3 a fin de
favorecer las tendencias de manejo más rápido que se practican en las curvas
mas suaves, es deseable que en ellas el peralte se aproxime al que obtiene
aplicando el método 3. El ministerios de obras públicas, en sus normas para el
proyecto de carreteras, adopta el criterio de establecer para cada radio, un
solo valor de peralte, basándose en la velocidad de circulación promedio que se
ha observado en las curvas de distintos radios, asumiendo una variación lineal
del coeficiente de rozamiento según la velocidad.
- PERALTE A PARTIR DEL VOLCAMIENTO:
Al dejar un alineamiento recto y al entrar en una curva, el vehículo,
empujado por la fuerza F con su punto de aplicación de las ruedas posteriores,
viene desviado en dirección de F.1 por las ruedas direccionales. Si se logra
mantener la componente F.2 de las de la fuerza en sentido circular de la curva,
el automóvil continuará su marcha dentro de los límites de la calzada, variando a cada instante la
componente bajo la acción de las ruedas direccionales. Las otras fuerzas actúan
al mismo tiempo sobre el vehículo; la fuerza centrífuga C que
tiende a volcar el vehículo, contrarrestada por el peso del vehículo P y por la
fuerza de adherencia y rozamiento del neumático con la superficie de la
pavimentación. Cuando la componente V cae afuera de las ruedas el automóvil
sufrirá un vuelco; si se consigue que la componente V no se salga fuera de las
ruedas, el vehículo proseguirá su marcha, pero para lograr esto es necesario
disminuir mucho la velocidad directriz con detrimento y perjuicio del transporte; se contrarresta entonces los peligros mencionados
con la construcción del peralte.
- PERALTE EN CONTRA CURVAS:
En ciertos casos el efecto de las solicitaciones transversales puede ser
el vuelco del vehículo, si las resultantes de las fuerzas que actúan sobre él
se sale fuera del polígono de sustentación formado por la punta de contacto de
las ruedas con el pavimento.
Designando con A el ancho de las ruedas y H la altura del centro de
gravedad sobre el pavimento, de un vehículo que se mueve a la velocidad V >
v sobre una curva de radio R, la condición de equilibrio para que no ocurra Volcamiento estará dada por
la igualdad de los momentos de W y F con relación a las
ruedas del lado exterior.
TRANSICIONES EN PERALTE:
A lo largo del tramo de carretera que precede al alineamiento curvo,
para pasar de una sección con bombeo a otra con peralte, es necesario efectuar
un cambio en la inclinación transversal de la calzada. Este cambio no puede
efectuarse bruscamente, sino que debe hacerse a través de un cambio gradual de
la pendiente de la calzada, haciéndose llamado transición del peraltado al
tramo de carretera en el cual se realiza.
Cuando en el proyecto de la carretera se han empleado curvas de
transición, la transición de peraltado se realiza conjuntamente con la de la
curvatura. En el caso en que no se emplee curvas de transición, la transición
del peraltado se realiza en la tangente y parte de la curva circular.
De las condiciones que debe reunir el trazado de una vía es la
seguridad, esta exige que cualquier obstáculo que se presente en la carretera
se advertido por el conductor con suficiente anticipación para actuar con bastante
tiempo sobre la dirección o sobre los frenos con el fin de evitar accidentes. El conductor debe disponer entonces de una
visibilidad suficiente, es decir; una longitud continua de carretera que
permita al conductor detenerse o desviarse a tiempo.
Se adopta como tiempo de percepción los siguientes valores
Velocidad en km/h tiempo de percepción
- 20 – 40 2
- 50 – 60 1,8
- 70 – 100 1,5
_Aplicación de la Flecha de Visibilidad:
La flecha de visibilidad es el ángulo que permítela conductor
desplazarse sin peligro de choque o que hace que mantenga una mayor visibilidad
en la vía principalmente en las curvas se aplica la fórmula:
donde:
F = flecha de visibilidad..
D = longitud continua de carretera.
R = radio de la curva.
Tasa constante de ascenso o descenso de una línea. Se expresa usualmente
en porcentaje; por ejemplo una pendiente del 4% es aquella que sube o baja 4
metros en una distancia horizontal de 100 metros. Cuando existen pendientes
longitudinales no es conveniente que se anule la transversal, como en algunos
casos se hace, porque entonces el agua seguirá la
dirección del eje de la vía, deteriorará el firme y podría llegar a molestar el
tráfico. Se prescribe, en general, que el agua tenga que
recorrer longitudinalmente, como máximo, el doble del ancho de la vía.
-Pendiente Máxima:
El valor absoluto de la pendiente no puede exceder nunca a un valor
máximo especificado. En todo momento se calcula el valor de la pendiente
necesaria para alcanzar la cota tentativa, y si este sobrepasa el máximo
permitido. La longitud de la pendiente máxima no debe sobrepasar tampoco cierto
valor especificado.
Las pendientes máximas a permitir en una carretera, están supeditada a
la velocidad del proyecto y a la composición del tráfico.
Los siguientes son los valores máximos admisibles:
- Velocidad del proyecto(Km/h) 50 65 80 95 110.
- Pendiente máxima(%) 6 – 8, 5 – 7, 4 – 6, 3 – 6, 3 – 5.
-Pendientes Mínimas:
Se admiten tramos horizontales (pendiente de cero %) siempre que la
sección transversal no presente problemas de
drenaje longitudinal. Donde se requiera drenar longitudinalmente la pendiente
mínima de la carretera debe asegurarse un drenaje satisfactorio. Salvo en casos
especiales, las pendientes no deben ser menores que los valores de la siguiente
tabla:
- Drenaje longitudinal pendiente mínima (%).
- Cuneta sin revestir 0,5.
- Canal – drenaje 0,4.
- Cuneta revestida 0,3.
- Brocal 0,3.
SOBREANCHO.
SOBREANCHO DE VÍA Y SU TRANSICIÓN.
El sobreancho se introduce
en las curvas horizontales para mantener las mismas condiciones de seguridad
que los tramos rectos, en cuanto al cruce de vehículos de sentido contrario,
por las siguientes razones:
El vehículo al describir la curva, ocupa mayor ancho que en la
tangente, esto es debido a que las ruedas traseras recorren una trayectoria
ubica en el interior de la descrita por las ruedas delanteras. Además, el
extremo delantero izquierdo, describe la trayectoria exterior del vehículo.
La dificultad que experimentan los conductores para mantenerse
en el eje del carril recorrido debido a la menor facilidad de apreciar la
posición relativa de sus vehículos dentro de la curva.
Sabiendo que si un vehículo va a
baja velocidad, el sobreancho se podría describir geométricamente, ya que el
eje posterior es radial, lo mismo ocurriría cuando describiera una curva
peraltada a una velocidad de equilibrio tal, de manera que la fuerza centrifuga
quedara completamente contrarrestada por la acción del peralte. En cambio si la
velocidad fuera menor o mayor que la velocidad de equilibrio, las ruedas
traseras se moverían a lo largo de una trayectoria mas cerrada o mas abierta,
respectivamente. Por lo expuesto la posición relativa de las ruedas traseras
depende de la velocidad, y no existe forma analítica de calcular el
desplazamiento entre las trayectorias de las ruedas delanteras y las traseras,
ya que de ello depende el ángulo de esviaje desarrollado por el vehículo. Para
determinar el valor del sobreancho, debe elegirse el vehículo representativo o
promedio del transito de la vía. Cuando el valor del sobreancho sea menor de 30
centímetros (0.30 metros) no es obligatoria su aplicación. Hay que tomar en
cuenta que si la curva horizontal consta de una espiral de transición, el sobre
ancho se reparte en ambos lados de la vía y que si la curva horizontal no
consta de una espiral de transición, el sobreancho se repartirá solo del lado
interior de esta.

BANQUETA DE VISIBILIDAD.
Las curvas horizontales deberán proyectarse manteniendo en toda su longitud la distancia de visibilidad de parada. En caso de no cumplir este requisito debido a la topografía, se proyectaran banquetas de visibilidad siguiendo algunos diseños.
En las Curvas Horizontales deberán asegurarse la Visibilidad a la distancia mínima de parada. El control de este requisito y determinación de la eventual banqueta de visibilidad se definirá, luego de verificar si una curva provee o no la distancia de visibilidad requerida, si la verificación indica que no se tiene la visibilidad requerida y no es posible o económico aumentar el radio de la curva.






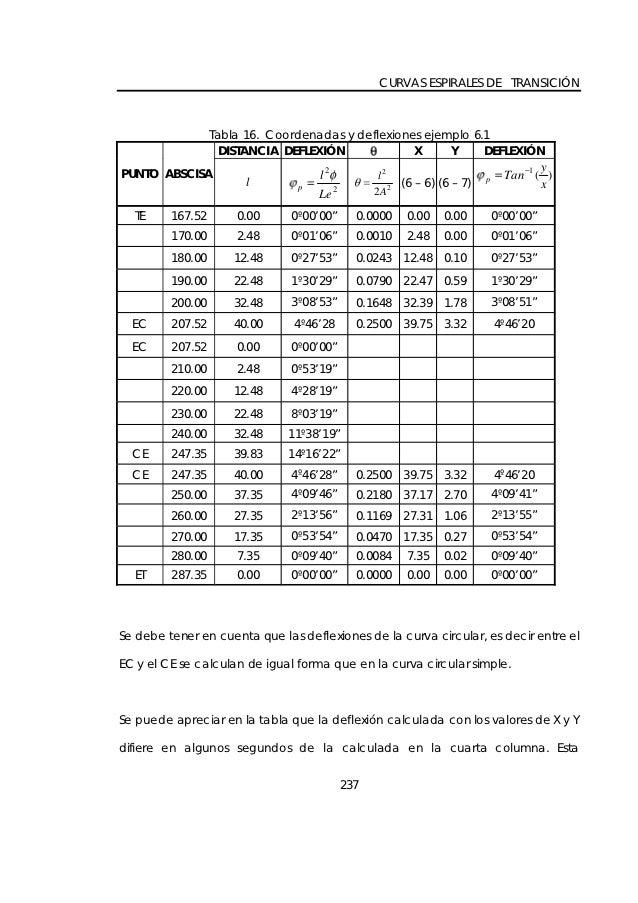




















![ Tangente [T]: Distancia desde el punto de intersección de las tangentes (PI) -los
alineamientos rectos también se conoce...](https://image.slidesharecdn.com/elementosdelacurvacircularessimplesparaunavia-150126051508-conversion-gate02/95/elementos-de-la-curva-circulares-simples-para-una-via-2-638.jpg?cb=1422249371)
![ Ordenada Media [M] (o flecha [F]): Distancia desde el punto medio de la curva hasta
el punto medio de la cuerda larga.
𝑀...](https://image.slidesharecdn.com/elementosdelacurvacircularessimplesparaunavia-150126051508-conversion-gate02/95/elementos-de-la-curva-circulares-simples-para-una-via-3-638.jpg?cb=1422249371)






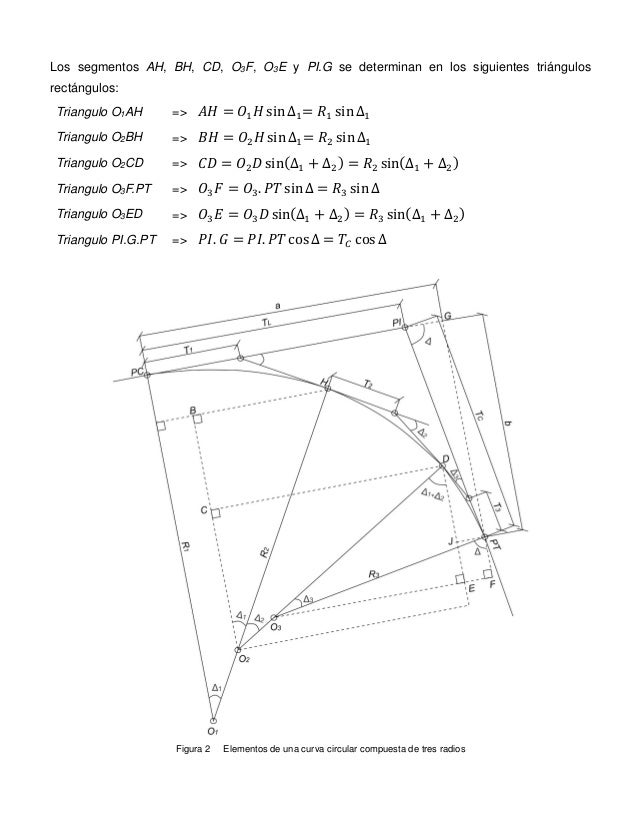
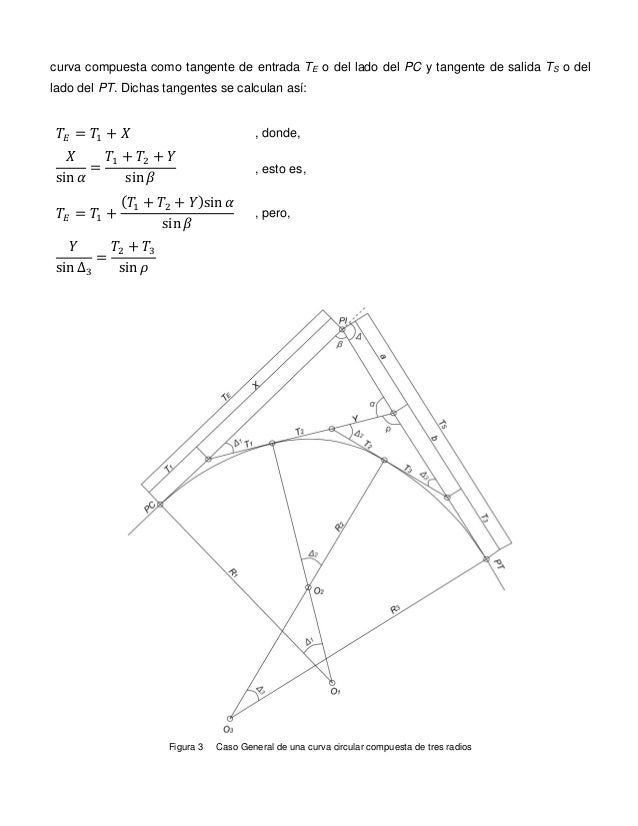
![Por lo tanto, en [1]:
𝑇𝑇𝐿𝐿 = 𝑅𝑅1 sin ∆1 − 𝑅𝑅2 sin ∆1 + 𝑅𝑅2 sin(∆1 + ∆2) + 𝑅𝑅3 sin ∆ − 𝑅𝑅3 sin(∆1 + ∆2) − 𝑇𝑇𝐶𝐶 cos ∆
𝑇𝑇𝐿𝐿 =...](https://image.slidesharecdn.com/curvascompuestas-robingomez9799075-160806002815/95/curvas-compuestas-robin-gomez-9799075-8-638.jpg?cb=1470443390)
![La tangente larga TL se obtiene reemplazando la ecuación (1-01) en [2]:
𝑇𝑇𝐿𝐿 = (𝑅𝑅1 − 𝑅𝑅2) sin ∆1 + (𝑅𝑅2 − 𝑅𝑅3) sin(∆1 + ∆...](https://image.slidesharecdn.com/curvascompuestas-robingomez9799075-160806002815/95/curvas-compuestas-robin-gomez-9799075-9-638.jpg?cb=1470443390)




 es la longitud de la muestra de roca.
es la longitud de la muestra de roca. es la longitud del camino electrolítico equivalente.
es la longitud del camino electrolítico equivalente.







